The “Most Hated” CSS Characteristic: cos() and sin()

No function is actually “the worst” in CSS, proper? In any case, it’s all primarily based on opinion and private expertise, but when we needed to attain a consensus, checking the State of CSS 2025 outcomes could be an excellent start line. I did precisely that, jumped into the awards part, and there I discovered it: the “Most Hated Characteristic,” a title no CSS ought to have bear…

This shocks me, if I’m being sincere. Are actually trigonometric capabilities actually that hated? I do know “hated” just isn’t the identical as saying one thing is “worst”, nevertheless it nonetheless has an terrible ring to it. And I do know I’m being somewhat dramatic right here, since solely “9.1% of respondents actually hate trigonometry.” However that’s nonetheless an excessive amount of shade being thrown for my style.

I need to get rid of that 9.1%. So, on this sequence, I need to have a look at sensible makes use of for CSS trigonometric capabilities. We’ll sort out them in items as a result of there’s so much to soak up and I discover it best to be taught and retain info when it’s chunked into targeted, digestible items. And we’ll begin with what could also be the most well-liked capabilities of the “worst” function: sin() and cos().

What the heck are cos() and sin() anyway?

This part is for many who cos() and sin() don’t fairly click on but, or just desire a refresher. For those who aced trigonometry quizzes in highschool, be at liberty to skip forward to the subsequent part!

What I discover humorous about cos() and sin()— and in addition why I feel there may be confusion round them — is the numerous methods we are able to describe them. We don’t should look too onerous. A fast look at this Wikipedia web page has an eye-watering variety of tremendous nuanced definitions.

This can be a studying drawback within the internet growth area. I really feel like a few of these definitions are far too normal and lack element concerning the essence of what trigonometric capabilities like sin() and cos() can do. Conversely, different definitions are overly advanced and educational, making them powerful to grok with out a sophisticated diploma.

Let’s stick with the candy center spot: the unit circle.

Meet the unit circle. It’s a circle with a radius of 1 unit:

Proper now it’s alone… in house. Let’s place it on the Cartesian coordinate system (the traditional chart with X and Y axes). We describe every level in house in Cartesian coordinates:

1. The X coordinate: The horizontal axis, plotting the purpose in the direction of the left or proper.
2. The Y coordinate: The vertical axis, plotting the purpose in the direction of the highest or backside.

We are able to transfer by the unit circle by an angle, which is measured from the optimistic X-axis going counter-clockwise.

We are able to go in a clockwise route by utilizing unfavorable angles. As my physics instructor used to say, “Time is unfavorable!”

Discover how every angle lands on a singular level within the unit circle. How else can we describe that time utilizing Cartesian coordinates?

When the angle is 0° the X and Y coordinates are 1 and 0 (1, 0), respectively. We are able to deduce the Cartesian coordinates for different angles simply as simply, like 90°, 180° and 270°. However for some other angle, we don’t know the place the purpose is initially positioned on the unit circle.

If solely there have been a pair of capabilities that take an angle and provides us our desired coordinates…

You guessed it, the CSS cos() and sin() capabilities do precisely that. They usually’re very intently associated, the place cos() is designed to deal with the X coordinate and sin() returns the Y coordinate.

Play with the toggle slider within the following demo to see the connection between the 2 capabilities, and see how they kind a proper triangle with the preliminary level on the unit circle:

I feel that’s all you actually need to learn about cos() and sin() for the second. They’re mapped to Cartesian coordinates, which permits us to trace a degree alongside the unit circle with an angle, it doesn’t matter what measurement that circle occurs to be.

Let’s dive into what we are able to truly use cos() and sin() for our on a regular basis CSS work. It’s all the time good to place somewhat real-world context to theoretical ideas like math.

Round layouts

If we go by the unit circle definition of cos() and sin(), then it’s straightforward to see how they is likely to be used to create round layouts in CSS. The preliminary setup is a single row of round parts:

Say we need to place every round merchandise across the define of a bigger circle as an alternative. First, we might let CSS know the entire variety of parts and in addition every factor’s index (the order it’s in), one thing we are able to do with an inline CSS variable that holds every order within the place:

<ul fashion="--total: 9">
  <li fashion="--i: 0">0</li>
  <li fashion="--i: 1">1</li>
  <li fashion="--i: 2">2</li>
  <li fashion="--i: 3">3</li>
  <li fashion="--i: 4">4</li>
  <li fashion="--i: 5">5</li>
  <li fashion="--i: 6">6</li>
  <li fashion="--i: 7">7</li>
  <li fashion="--i: 8">8</li>
</ul>

Word: This step will change into a lot simpler and concise when the sibling-index() and sibling-count() capabilities achieve assist (and they’re actually neat). I’m hardcoding the indexes with inline CSS variables within the meantime.

To put the objects across the define of a bigger circle, we’ve to house them evenly by a sure angle. And to get that angle, we are able to divide 360deg (a full flip across the circle) by the entire variety of objects, which is 8 on this particular instance. Then, to get every factor’s particular angle, we are able to multiply the angle spacing by the factor’s index (i.e., place):

li {
  --rotation: calc(360deg / var(--total) * var(--i));
}

We additionally have to push the objects away from the middle, so we’ll assign a --radius worth for the circle utilizing one other variable.

ul {
  --radius: 10rem;
}

We now have the factor’s angle and radius. What’s left is to calculate the X and Y coordinates for every merchandise.

That’s the place cos() and sin() come into the image. We use them to get the X and Y coordinates that place every merchandise across the unit circle, then multiply every coordinate by the --radius worth to get an merchandise’s closing place on the larger circle:

li {
  /* ... */
  place: absolute;

  remodel: translateX(calc(cos(var(--rotation)) * var(--radius))) 
             translateY(calc(sin(var(--rotation)) * var(--radius)));
}

That’s it! We now have a sequence of eight round objects positioned evenly across the define of a bigger circle:

And we didn’t want to make use of a bunch of magic numbers to do it! All we offer CSS with is the unit circle’s radius, after which CSS does all of the trigonometric gobbledygook that makes so many people name this the “worst” CSS function. Hopefully, I’ve satisfied you to melt your opinions on them if that’s what was holding you again!

We aren’t restricted to full circles, although! We are able to even have a semicircular association by selecting 180deg as an alternative of 360deg.

This opens up a lot of format potentialities. Like, what if we wish a round menu that expands from a middle level by transitioning the radius of the circle? We are able to completely do this:

Click on or hover the heading and the menu objects kind across the circle!

Wavy layouts

There’s nonetheless extra we are able to do with layouts! If, say, we plot the cos() and sin() coordinates on a two-axis graph, discover how they offer us a pair of waves that periodically go up and down. And spot they’re offset from one another alongside the horizontal (X) axis:

The place do these waves come from? If we predict again to the unit circle we talked about earlier, the worth of cos() and sin() oscillate between -1 and 1. In different phrases, the lengths match when the angle across the unit circle varies. If we graph that oscillation, then we’ll get our wave and see that they’re sorta like reflections of one another.

⚠️ Auto-playing media

Can we place a component following certainly one of these waves? Completely. Let’s begin with the identical single row format of round objects we made earlier. This time, although, the size of that row spans past the viewport, inflicting overflow.

We’ll assign an index place for every merchandise like we did earlier than, however this time we don’t have to know the entire variety of objects. We had eight objects final time, so let’s bump that as much as 10 and faux like we don’t know that:

<ul>
  <li fashion="--i: 0"></li>
  <li fashion="--i: 1"></li>
  <li fashion="--i: 2"></li>
  <li fashion="--i: 3"></li>
  <li fashion="--i: 4"></li>
  <li fashion="--i: 5"></li>
  <li fashion="--i: 6"></li>
  <li fashion="--i: 7"></li>
  <li fashion="--i: 8"></li>
  <li fashion="--i: 9"></li>
  <li fashion="--i: 10"></li>
</ul>

We need to fluctuate the factor’s vertical place alongside both a sin() or cos() wave, which means translating every merchandise’s place primarily based on its order within the index. We’ll multiply an merchandise’s index by a sure angle that’s handed into the sin() perform, and that may return a ratio that describes how excessive or low the factor must be on the wave. The ultimate factor is to multiply that end result by a size worth, which I calculated as half an merchandise’s complete measurement.

Right here’s the mathematics in CSS-y phrases:

li {
  remodel: translateY(calc(sin(60deg * var(--i)) * var(--shape-size) / 2));
}

I’m utilizing a 60deg worth as a result of the waves it produces are smoother than another values, however we are able to fluctuate it as a lot as we need to get cooler waves. Mess around with the toggle within the subsequent demo and watch how the wave’s depth modifications with the angle:

This can be a nice instance to see what we’re working with, however how would you employ it in your work? Think about we’ve two of those wavy chains of circles, and we need to intertwine them collectively, kinda like a DNA strand.

Let’s say we’re beginning with the HTML construction for 2 unordered lists nested inside one other unordered listing. The 2 nested unordered lists symbolize the 2 waves that kind the chain sample:

<ul class="waves">
  <!-- First wave -->
  <li>
    <ul class="principal">
      <!-- Circles -->
      <li fashion="--i: 0"></li>
      <li fashion="--i: 1"></li>
      <li fashion="--i: 2"></li>
      <li fashion="--i: 3"></li>
      <!-- and many others.  -->
    </ul>
  </li>

  <!-- Second wave -->
  <li>
    <ul class="secondary">
      <!-- Circles -->
      <li fashion="--i: 0"></li>
      <li fashion="--i: 1"></li>
      <li fashion="--i: 2"></li>
      <li fashion="--i: 3"></li>
      <!-- and many others.  -->
    </ul>
  </li>
</ul>

Fairly just like the examples we’ve seen up to now, proper? We’re nonetheless working with an unordered listing the place the objects are listed with a CSS variable, however now we’re working with two of these lists… and so they’re contained inside a 3rd unordered listing. We don’t should construction this as lists, however I made a decision to depart them so I can use them as hooks for added styling later.

To keep away from any issues, we’ll ignore the 2 direct <li> parts within the outer unordered listing that include the opposite lists utilizing show: contents.

.waves > li { show: contents; }

Discover how one of many chains is the “principal” whereas the opposite is the “secondary.” The distinction is that the “secondary” chain is positioned behind the “principal” chain. I’m utilizing barely totally different background colours for the objects in every chain, so it’s simpler to differentiate one from the opposite as you scroll by the block-level overflow.

We are able to reorder the chains utilizing a stacking context:

.principal {
  place: relative;
  z-index: 2;
}

.secondary { place: absolute; }

This positions one chain on high of the opposite. Subsequent, we’ll alter every merchandise’s vertical place with the “hated” sin() and cos() capabilities. Bear in mind, they’re sorta like reflections of each other, so the variance between the 2 is what offsets the waves to kind two intersecting chains of things:

.principal {
  /* ... */
  li {
    remodel: translateY(calc(sin(60deg * var(--i)) * var(--shape-size) / 2));
  }
}

.secondary {
  /* ... */
  li {
    remodel: translateY(calc(cos(60deg * var(--i)) * var(--shape-size) / 2));
  }
}

We are able to intensify the offset much more by shifting the .secondary wave one other 60deg:

.secondary {
  /* ... */
  li {
    remodel: translateY(calc(cos(60deg * var(--i) + 60deg) * var(--shape-size) / 2));
  }
}

The subsequent demo exhibits how the waves intersect at an offset angle of 60deg. Modify the slider toggle to see how the waves intersect at totally different angles:

Oh, I instructed you this may very well be utilized in a sensible, real-world approach. How about including somewhat whimsy and aptitude to a hero banner:

Damped oscillatory animations

The final instance obtained me pondering: is there a approach to make use of sin() and cos()‘s forwards and backwards motion for animations? The primary instance that got here to thoughts was an animation that additionally went forwards and backwards, one thing like a pendulum or a bouncing ball.

That is, after all, trivial since we are able to do it in a single animation declaration:

.factor {
  animation: someAnimation 1s infinite alternate;
}

This “forwards and backwards” animation known as oscillatory motion. And whereas cos() or sin() are used to mannequin oscillations in CSS, it could be like reinventing the wheel (albeit a clunkier one).

I’ve realized that excellent oscillatory motion — like a pendulum that swings forwards and backwards in perpetuity, or a ball that by no means stops bouncing — doesn’t actually exist. Motion tends to decay over time, like a bouncing spring:

⚠️ Auto-playing media

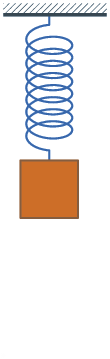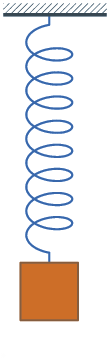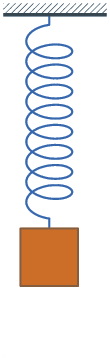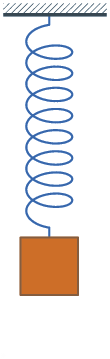
There’s a selected time period that describes this: damped oscillatory motion. And guess what? We are able to mannequin it in CSS with the cos() perform! If we graph it over time, then we’ll see it goes forwards and backwards whereas getting nearer to the resting place¹.

Wikipedia has one other animated instance that properly demonstrates what damped oscillation seems like.

Basically, we are able to describe damped oscillation over time as a mathematical perform:

It’s composed of three elements:

• e^−γt: Because of the unfavorable exponent, it turns into exponentially smaller as time passes, bringing the motion to a gradual cease. It’s multiplied by a damping fixed (γ) that specifies how rapidly the motion ought to decay.
• a: That is the preliminary amplitude of the oscillation, i.e., the factor’s preliminary place.
• cos(ωt−α): This provides the motion its oscillation as time passes. Time is multiplied by frequency (ω), which determines a component’s oscillation pace². We are able to additionally subtract from time α, which we are able to use to offset the preliminary oscillation of the system.

Okay, sufficient with all the idea! How will we do it in CSS? We’ll set the stage with a single circle sitting all by itself.

We now have a number of CSS variables we are able to outline that may come in useful since we already know the components we’re working with:

:root {
  --circle-size: 60px;

  --amplitude: 200px; /* The amplitude is the space, so let's write it in pixels*/
  --damping: 0.3;
  --frequency: 0.8;
  --offset: calc(pi/2); /* This is identical as 90deg! (However in radians) */
}

Given these variables, we are able to peek at what the animation would seem like on a graph utilizing a software like GeoGebra:

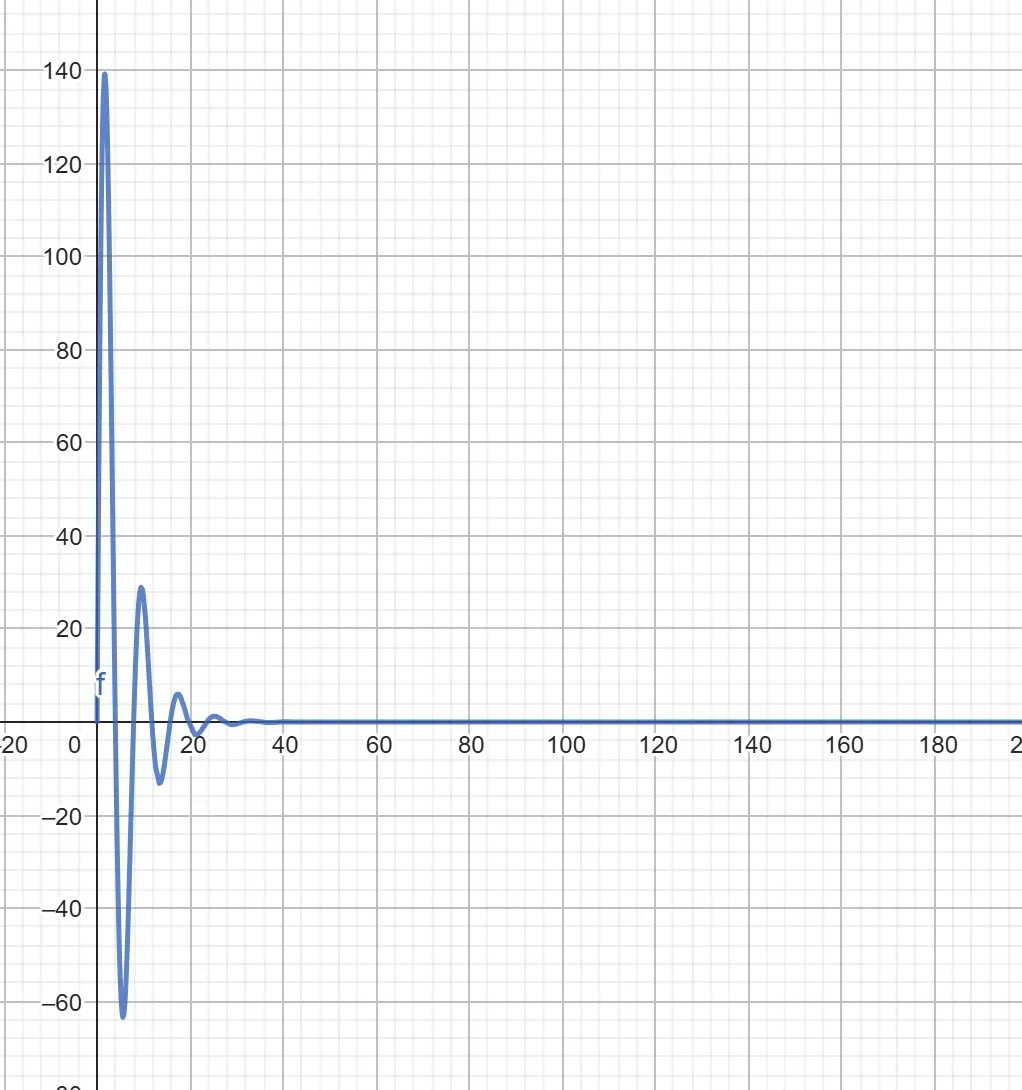
From the graph, we are able to see that the animation begins at 0px (due to our offset), then peaks round 140px and dies out round 25s in. I, for one, gained’t be ready 25 seconds for the animation to finish, so let’s create a --progress property that may animate between 0 to 25, and can act as our “time” within the perform.

Do not forget that to animate or transition a customized property, we’ve gotta register it with the @property at-rule.

@property --progress {
  syntax: "<quantity>";
  initial-value: 0;
  inherits: true;
}

@keyframes motion {
  from { --progress: 0; }
  to { --progress: 25; }
}

What’s left is to implement the prior components for the factor’s motion, which, written in CSS phrases, seems like this:

.circle {
  --oscillation: calc(
    (exp(-1 * var(--damping) * var(--progress))) * 
    var(--amplitude) * 
    cos(var(--frequency) * (var(--progress)) - var(--offset))
  );

  remodel: translateX(var(--oscillation));
  animation: motion 1s linear infinite;
}

This provides a fairly satisfying animation by itself, however the damped movement is just on the x-axis. What would it not seem like if, as an alternative, we utilized the damped movement on each axes? To do that, we are able to copy the identical oscillation components for x, however exchange the cos() with sin().

.circle {
  --oscillation-x: calc(
    (exp(-1 * var(--damping) * var(--progress))) * 
    var(--amplitude) * 
    cos(var(--frequency) * (var(--progress)) - var(--offset))
  );
  --oscillation-y: calc(
    (exp(-1 * var(--damping) * var(--progress))) * 
    var(--amplitude) * 
    sin(var(--frequency) * (var(--progress)) - var(--offset))
  );

  remodel: translateX(var(--oscillation-x)) translateY(var(--oscillation-y));
  animation: motion 1s linear infinite;
}

That is much more satisfying! A round and damped movement, all due to cos() and sin(). Apart from wanting nice, how may this be utilized in an actual format?

We don’t should look too onerous. Take, for instance, this sidebar I just lately made the place the menu objects pop within the viewport with a damped movement:

Fairly neat, proper?!

Extra trigonometry to return!

Effectively, discovering makes use of for the “most hated CSS function” wasn’t that arduous; perhaps we should always begin displaying some like to trigonometric capabilities. However wait. There are nonetheless a number of trigonometric capabilities in CSS we haven’t talked about. Within the following posts, we’ll preserve exploring what trig capabilities (like tan() and inverse capabilities) can do in CSS.

Additionally, earlier than I neglect, right here is one other demo I made utilizing cos() and sin() that didn’t make the lower on this article, however it’s nonetheless price trying out as a result of it dials up the swirly-ness from the final instance to indicate how wacky we are able to get.

Footnotes

1. This sort of damped oscillatory motion, the place the forwards and backwards is extra seen, known as underdamped oscillation. There are additionally overdamped and critically damped oscillations, however we gained’t concentrate on them right here. ↪️
2. In actuality, the damped fixed and the frequency are intently associated. You’ll be able to learn extra about damped oscillation in this paper. ↪️

The “Most Hated” CSS Characteristic: cos() and sin() initially printed on CSS-Tips, which is a part of the DigitalOcean household. It’s best to get the publication.